正则化网络

2.给定一个感知器网络$f(\mathbf x)=\sum _{i=0}^n w_i \varphi _i(\mathbf w_i ^\mathrm{T}\mathbf x)$，其中$\varphi_i(\cdot)$为Logistic 型激活函数。 和一个广义正则化网络$f_\lambda(x)=\sum _{i=1}^n w_iG(\mathbf x,\mathbf x_i)$，其中$G(\mathbf x,\mathbf x_i)$为以数据点$\mathbf x_i$为中心的径向基函数。请: (1) 画出该感知器网络和广义正则化网络的结构图; (2) 分析两个模型在不同方面的异同; (3) 尝试估计正则化网络的VC维。

（1）

输入信号：$\mathbf x_i \in \mathbb R^m, i=1,2,\ldots ,N$ 预期输出：$d_i \in \mathbb R ,i=1,2,\ldots ,N$

感知器网络:

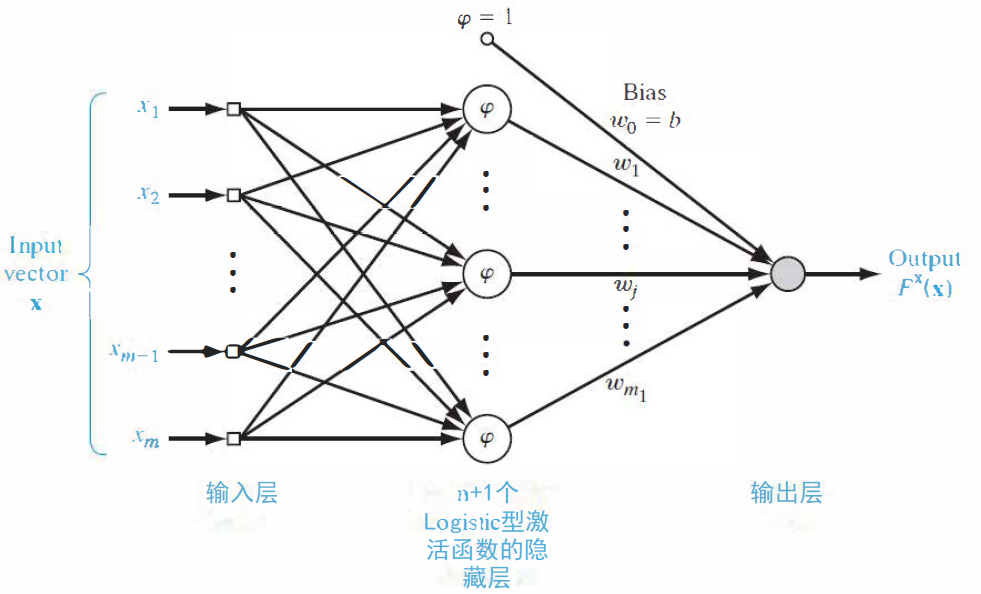
广义正则化网络:

• 输入层：共$m$个结点，$m$为输入向量$\mathbf x$的维数。
• 隐藏层：共$N$个结点，每一个数据点$\mathbf x_i$，$i=1,2,\ldots ,N$都对应一个隐藏层结点，$N$为样本数量。第$i$个结点的输出为$G(\mathbf x,\mathbf x_i)$。
• 输出层：和隐藏层全连接的单个线性单元。

（2）

• 拟合能力：正则化网络只要有足够多的隐藏单元，可以以任意精度逼近定义在$\mathbb R^m$的compact subset上的任意多元连续函数。

（3）

正则化网络中的参数个数为$(m+1)N$，因此估计其VC维为$(m+1)N$。