神经网络入门

Multi-Layer Neural Network

A. 3-layer network: Input Layer,Hidden Lyer,Output layer. Except input units,each unit has a bias.

preassumption calculation

$\begin{aligned} net_{j} = \sum_{i=1}^{d}x_{i}w_{ji}+w_{j0}=\sum_{i=0}^{d}x_{i}w_{ji}=w_{j}^{t}x \end{aligned}$

Specifically, a signal $x{i}$ at the input of synapse $i$ connected to nueron $j$ us multiplied by the synaptic weight $w{ji}$. $i$ refers input layer,$j$ refers hidden layer.$w{j0}$ is the bias.$x{0}=+1$.

Each neuron is represented by a set of linear synaptic links, an externally applied bias, and a possibly nonlinear activation link.The bias is represented by a synaptic link connected to an input fixed at $+1$.
The synaptic links of a neuron weight their respective input signals.
The weighted sum of the input signals defines the induced local field of the neuron in question.
The activation link squashes the induced local field of the neuron to produce an output. Output layer:

$\begin{aligned} y_{j}=f(net_{j}) \end{aligned}$

$f()$ is the activation function.It defines the output of a neuron in terms of the induced local field $net$ .

{% math %}
\begin{matrix}
 x_{0}=+1 \ar[ddr]|(0.6){w_{j0}} &  &  \\
 x_{1} \ar[r]|(0.6){w_{j1}} & B & C \\
 x_{2} \ar[r]^(0.6){w_{j2}} & net_{j} \ar[r]^(0.6){f()} & y_{j} \\
 x
\end{matrix}
{% endmath %}

For example: $\begin{aligned} net_{k}=\sum_{j=1}^{n_{H}}y_{i}w_{kj}+w_{k0}=\sum_{j=0}^{n_{H}}x_{i}w_{ji}=w_{k}^{t}y \end{aligned}$ $n_{H}$is the number of hidden layers.

So: $\begin{aligned} g_{k}(x)=f(\sum_{j=1}^{n_{H}}w_{kj}+f(\sum_{i=0}^{d}x_{i}w_{ji}+w_{j0})+w_{k0}) \end{aligned}$ The activate function of output layer can be different from hidden layer while each unit can have different activate function.

BP Algorithm

The popularity of on-line learning for the supervised training of multilayer perceptrons has been further enhanced by the development of the back-propagation algorithm. Backpropagation, an abbreviation for "backward propagation of errors",is the easiest way of supervised training.We need to generate output activations of each hidden layer. The partial derivative $\partial J /\partial w{ji}$ represents a sensitivity factor, determining the direction of search in weight space for the synaptic weight $ w{ji}$. Learning: $\begin{aligned} \mathcal T =\{ x(n),d(n)\}_{n=1}^{N}\\ e_{j}(n)=d_{j}(n)-y_{j}(n) \end{aligned}$ the instantaneous error energy of neuron $j$ is defined by $\begin{aligned} J(w)=\frac 12 \sum_{k=1}^{c}(e_{k})^{2}=\frac 12||t-\delta||^{2} \\ \end{aligned}$ In the batch method of supervised learning, adjustments to the synaptic weights of the multilayer perceptron are performed after the presentation of all the $N$ examples in the training sample $\mathcal T$ that constitute one epoch of training. In other words, the cost function for batch learning is defined by the average error energy $J(w)$.

firstly define the training bias of output layer: $\begin{aligned} \Delta w=-\eta\frac {\partial J(w)}{\partial w} \\ w(m+1)=w(m)+/Delta w(m) \end{aligned}$

$\begin{aligned} \frac {\partial J}{\partial w_{kj}}=\frac {\partial J}{\partial net_{k}}\frac {\partial net_{k}}{\partial w_{kj}} \\ \frac {\partial J}{\partial net_{k}}= \frac {\partial J}{\partial \delta _{k}}\frac {\partial \delta _{k}}{\partial J}=-(t_{k}-\delta _{k})f'(net_{k}) \\ \Delta w_{kj}=\eta \frac {\partial J}{\partial net_{k}}=\eta (t_{k}-\delta _{k}))f'(net_{k})y_{j} \end{aligned}$

input->hidden

High dimension：

SVM ,拟合能力随维度增加线性增长
kenel-based,内积
易收敛
convex
low computational cost

Going deep：神经网络，拟合能力随深度增加指数增长

复杂boundary
non-convex
Black-magic
overfitting
High computational cost
矩阵联乘

1.神经网络获取的知识是从外界环境中学习得来的； 2.互连神经元的连接强度，即突触权值，用于储存获取的知识。

神经网络的功能 |功能 |神经网络 | | :------: | :----- | |分类|单层感知器、线性神经网络、BP神经网络、RBF神经网络、CNN、DBN、LVQ神经网络、Elman神经网络| |拟合|BP神经网络、RBF神经网络、DBN、Elman神经网络| |聚类|通用型竞争神经网络、SOM神经网络| |特征表示|RBM、Word2vec、CNN| |记忆|离散型Hopfield网络、Elman神经网络| |最优化求解|连续型Hopfield神经网络|

神经元

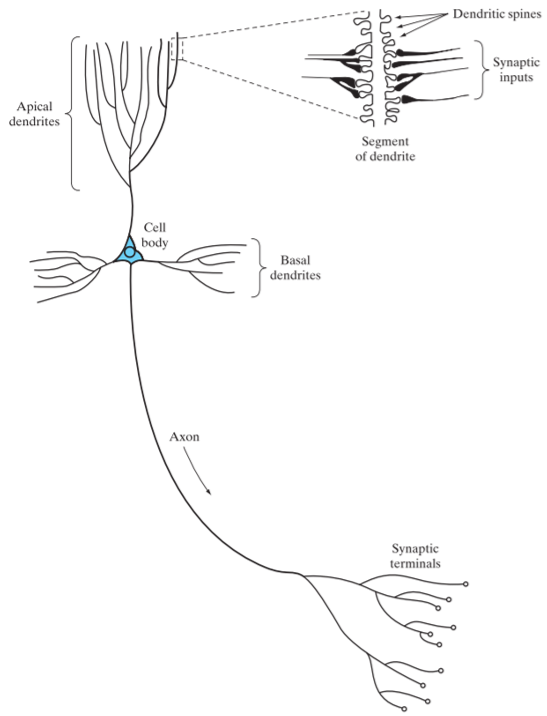
线性神经元

$\begin{aligned} y=\varphi(\sum _{i=0}^mw_ix_i )=\varphi( \mathbf w^T \mathbf x)\\ \varphi(v)=v \end{aligned}$

非线性神经元——感知器 (perceptron)

$\varphi(v)=\frac 1{1+e^{-v}}$

人工神经元模型： 1940年McCulloch与Pitts提出仿造神经元的人工神经元模型。神经元网络的输入端接收多维输入向量（如模式识别中常用的特征向量），输出端只有一个。该模型由两部分功能组成，一部分功能将输入端信号进行线性迭加，另一部分是对该迭加值进行非线性映射及从输出端输出。 McCulloch-Pitts模型中的非线性映射是阈值函数，输入值从负无穷到某个值内输出为0，输入一旦达到该阈值，输出为1。这种0—1输出也可改成-1—+1输出。近来人们根据需要, 在人工神经元模型中也采用其它类型的非线性映射。
- McCulloch-Pitts模型：就是McCulloch和Pitts俩人在1940提出的人工神经元模型。
单层感知器：一个McCulloch-Pitts模型可实现的功能是两类别线性分类器，输入向量的线性求和是判别函数，非线性映射及输出的0、1值表示了分类结果。这种线性分类器的系数若采用感知准则函数方法确定，它就是一个感知器。这种感知器与多层感知器相比，只有一层，因而称为单层感知器。

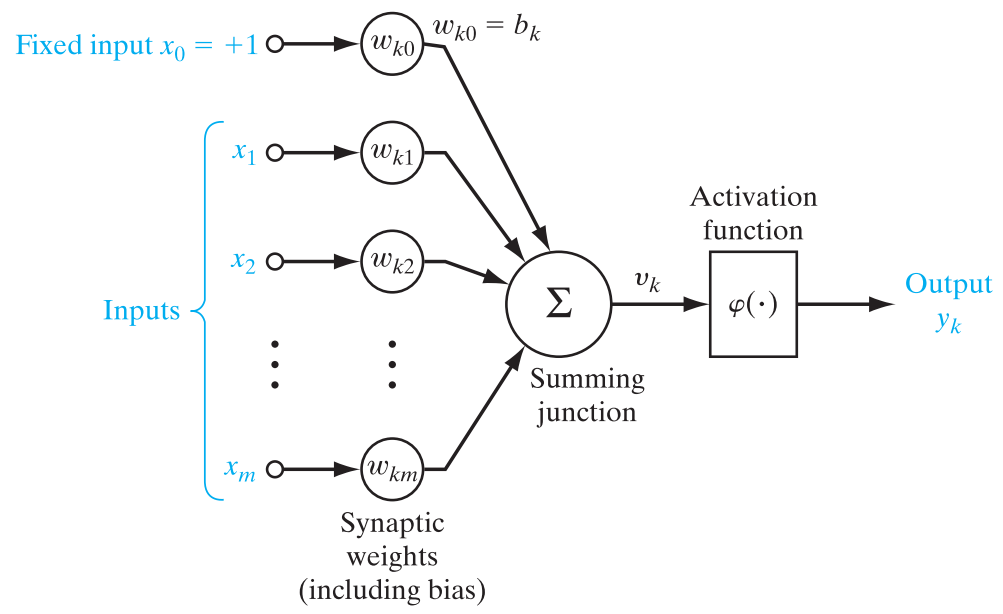
突触（权值）$w_{ki}$ 每一个都由其权值或者强度作为特征。特别是，在连接到神经元$k$的突触$j$上的输入信号被乘以$k$的突触权值。
偏置$w{k0}$, $x{0}=+1$
```
   用来调节值域的。
```
加法器是一个线性组合器，求输入信号与神经元相应突触权值的加权和，并与偏置求和。

$net_{k} = \sum_{i=1}^{m}x_{i}w_{ki}+w_{k0}=\sum_{i=0}^{m}x_{i}w_{ki}=w_{k}^{t}x$

多层前馈神经网络(Multi-Layer Neural Network)

特点：

每层神经元与下一层神经元全互联
解决非线性可分问题——多层功能神经元
前馈（feedforward）并不意味着网络中信号不能后传，而是指网络拓扑结构上不存在环或回路。
输入层仅是接受输入，不进行函数处理，隐层与输出层包含功能神经元
隐层结点：由两层及两层以上结点组成的前馈网络中处于非输出层的结点称为隐层结点，一个只含一个隐含层的前馈网络称为双层前馈网络。含两个隐含层的称三层前馈网络。一般使用至多两个隐含层的网络。

网络中传递的两种信号：

函数信号
- 来自于输入端，到达输出端
误差信号
- 产生于输出端，反向传播

每个神经元完成两种计算：

计算输出函数信号
- 输入信号和权值的连续非线性函数
计算梯度向量
- 误差曲面对于权值的梯度的估计

学习

神经网络的学习过程，就是根据训练数据来调整神经元之间的连接权（connection weight）以及每个功能神经元的阈值；换言之，神经网络“学”到的东西，蕴含在连接权与阈值中。

最小均方算法(LMS)

定义代价函数(cost function)为均方误差 $\varepsilon(w)=\frac 1{2N}\sum_{n=1}^N e^2(n)$ 其中$e(n)$为时刻$n$测得的误差。定义权值更新规则 $w\leftarrow w+\Delta w$ 基于最速下降法则 $\Delta w=-\frac {\partial \varepsilon (w)}{\partial w}=-\frac 1N\sum_{n=1}^N e( n)\frac {\partial e(n)}{\partial w}$ 要求激活函数可导。

批处理方式（batch）称为集中方式、批处理方式训练集内的全部样本都呈现一遍之后，才进行权值更新。这样称为一个回合（epoch）

定义代价函数(cost function)为瞬时误差的平方 $\varepsilon(w)=\frac 12 e^2(n)$ 在线学习（on-line）称为串行方式、在线方式、随机方式每个训练样本呈现之后，即进行权值更新. 训练集内的全部N个样本都呈现一次，称为一个回合(epoch)；

对于单层感知器来说： $C$是输出层的所有神经元

集中方式 $\varepsilon(w)=\frac 1{2N} \sum _{i=1}^N\sum _{k \in C}e_k^2(n)$
在线方式 $\varepsilon(w)=\frac 12 \sum _{k \in C}e_k^2(n)$

在单层感知器中误差信号是直接可以测量的在多层感知器中，隐层神经元是不可见的，其误差信号无法直接测量

感知机学习规则

对训练样例$(x,y)$,若当前感知机的输出为$\hat y$,则感知机权重将这样调整： $ \begin{aligned} w_i \leftarrow w_i+\Delta w_i \ \Delta w_i=\eta(y-\hat y)x_i \end{aligned} $ 其中$\eta \in (0,1)$称为学习率（learning rate），通常设置一个较小正数，如0.1.

感知机只有输出层神经元进行激活函数处理，即只拥有一层功能神经元（functional neuron），学习能力非常有限。若两类模式是线性可分的，即存在一个线性超平面能将他们分开，则感知机的学习过程一定会收敛（converge）而求得适当的权值向量$w=(w1;w_2;\ldots;w{n+1})$，否则感知机学习过程将发生震荡（fluctuation），$w$难以稳定下来，不能求得合适解。

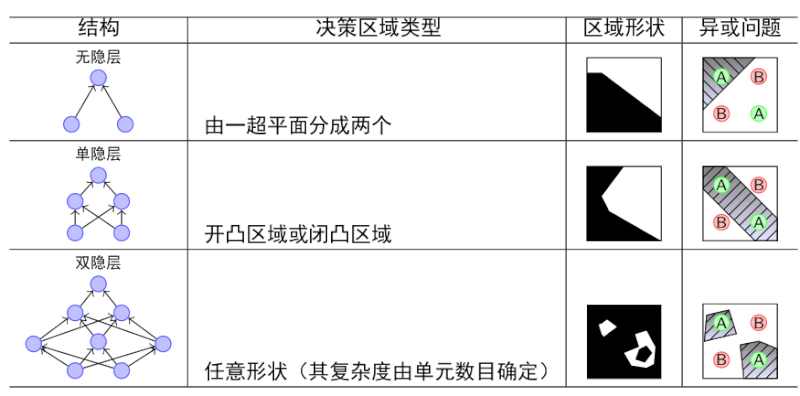
误差逆传播算法(error BackPropagation)

欲训练多层网络，简单感知机学习规则显然不够，需要更强大的学习算法，BP算法是其中最杰出的代表。有串行方式（on-line）和集中方式(batch)两种。 The popularity of on-line learning for the supervised training of multilayer perceptrons has been further enhanced by the development of the back-propagation algorithm. 它是基于误差修正学习规则的。误差反向传播学习由两次经过网络不同层的通过组成：一次前向通过和一次后向通过。在前向通过中，一个输入向量作用于网络感知节点，它的影响通过网络一层接一层的传播，最后产生一个输出作为网络的实际输出。在前行通过中，网络的突触权值全为固定的。另一方面，在反向通过中，网络的突触权值全部根据误差规则来调整。特别是从目标响应减去网络的实际响应为误差信号。这个误差信号反向传播经过整个网络，与突触连接方向相反因此叫“误差反向传播”。

工作流程 A 初始化 B 训练样本的呈现 C 信息前向计算 D 误差反向传播 E 判断终止条件并迭代

计算梯度

给定训练集$D={(x_1,y_1)，(x_2,y_2)，\ldots,(x_m,y_m)}$,$x_i \in \mathbb R^d$,$y_i \in \mathbb R^c$，即输入实例由d个属性描述，输出$c$维实值向量.

下图给出了一个拥有d个输入神经元、m个隐层神经元、c个输出神经元的多层前馈网络结构：

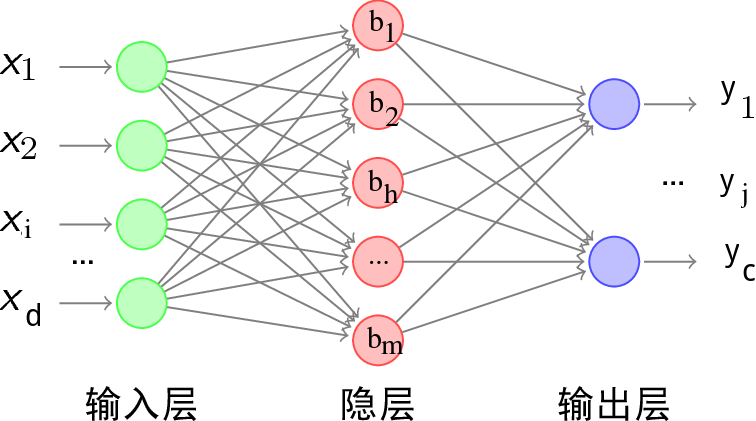
其中，

隐层第$h$个神经元的阈值用$\gamma _h$表示，
输出层第$j$个神经元的阈值用$\theta_j$表示。
输入层第$i$个神经元与隐层第$h$个神经元之间的连接权为$v_{ih}$;
隐层第$h$个神经元与输出层第$j$个神经元之间的连接权为$w_{hj}$;
记隐层第$h$个神经元接收到的输入为$\alphah=\sum{i=1}^dv_{ih}x_i$;
输出层第$j$个神经元接收到的输入为$\betaj=\sum{h=1}^mw_{hj}b_h$, 其中$b_h$为隐层第$h$个神经元的输出;
假设隐层和输出层神经元都使用Logistic函数： $P(t)=\frac 1{1+e^{-t}}$

输出层

以串行为例，对训练样本$（xk,y_k）$,假定神经网络的输出为$\hat y_k=（\hat y_1^k,\hat y_2^k,\ldots,\hat y_c^k）$,即 $\hat y_j^k=f(\beta_j-\theta_j),$ 则网络在$（x_k,y_k）$上的均方误差（LMS算法）为 $E_k=\frac 12\sum_{j=1}^c(\hat y_j^k-y_j^k)^2.$ 根据广义的感知机学习规则对参数进行更新，任意参数$v$的更新估计式为 $v \leftarrow v+\Delta v$ BP算法基于梯度下降策略，对误差$E_k$,给定学习率$\eta$,有 $\Delta w_{hj}=-\eta \frac {\partial E_k}{\partial w_{hj}}$ 考虑到$w{hj}$先影响到第$j$个输出层神经元的输入值$\betaj$，再影响到其输出值$\hat y_j^k$,最后影响到$E_k$,有 $\frac {\partial E_k}{\partial w_{hj}}=\frac {\partial E_k}{\partial \hat y_j^k}\frac {\partial \hat y_j^k}{\partial \beta _j}\frac {\partial \beta _j}{\partial w_{hj}}$ 根据$\beta_j$的定义，显然有 $\frac {\partial \beta _j}{\partial w_{hj}}=b_h$ 而Logistic函数有一个性质： $f'(x)=f(x)(1-f(x))$ 于是有 $g_j=-\frac {\partial E_k}{\partial \hat y_j^k}\frac {\partial \hat y_j^k}{\partial \beta _j} =-(\hat y_j^k-y_j^k)f'(\beta _j-\theta _j)=\hat y_j^k(1-\hat y_j^k)(y_j^k-\hat y_j^k).$ 于是得到了BP算法中关于$w{hj}$的更新公式 $\Delta w_{hj}=\eta g_j b_h$

隐层

根据（2）中的推导 $\begin{aligned} \Delta \theta_j&=-\eta\frac {\partial E_k}{\partial \hat y_j^k}\cdot\frac {\partial \hat y_j^k}{\partial \theta_j}\\ &=\eta(\hat y_j^k-y_j^k)f'(\beta _j-\theta _j)\\ &=-\eta g_j \end{aligned}$ $bh$为第$h$个隐层神经元的输出，即 $b_h=f(\alpha _h-\gamma _h)$ 考虑到$v{ih}$先影响到第$h$个隐层神经元的输入值$\alpha_h$，再影响到其输出值$b_h$,最后影响到$E_k$,有 $\frac {\partial E_k}{\partial v_{ih}}=\frac {\partial E_k}{\partial b_h}\cdot\frac {\partial b_h}{\partial \alpha _h}\cdot\frac {\partial \alpha_h}{\partial v_{ih}}$ 类似（2）中的$g_j$，有 $\begin{aligned} e_h&=-\frac {\partial E_k}{\partial b_h}\cdot\frac {\partial b_h}{\partial \alpha _h}\\ &=-\sum _{j=1}^c\frac {\partial E_k}{\partial \beta _j}\cdot \frac {\partial \beta _j}{\partial b_h}f'(\alpha_h-\gamma_h)\\ &=\sum _{j=1}^cw_{hj}g_jf'(\alpha_h-\gamma_h)\\ &=b_h(1-b_h)\sum_{j=1}^cw_{hj}g_j \end{aligned}$ 所以 $\Delta v_{ih}=\eta e_h x_i$ 另外,类似$\Delta \theta _j$ $\Delta \gamma_h=-\eta e_h$

其他常见神经网络

经向基函数网络

在多层感知器的人工神经元一般采用S型函数作非线性映射。而经向基函数网络则采用单峰型函数（如高斯函数）为非线性映射函数。在实现数据拟合等等应用中较多。训练也较简单。

Hopfield模型

是人工神经元网络中一个典型网络，该网络中的所有神经元实行全联接，即任一个神经元的输入输出都联接至其它结点的输入端，因此每一个结点的状态对其它结点的状态都有牵扯作用。该网络的联接数值由Hebb规则确定。其功能可实现联想记忆, 是人工神经网络中的一种动力系统。网络具有存储模式功能，有自己的稳态，其原理与电子线路中的双稳态触发器相仿。

自适应共振理论

自适应共振理论是Carpeter和Grossberg在1987年提出的网络模型，它主要模仿人积累知识的过程。例如人们可以辩别当前见到的事物, 是已往见到过的事物，还是从未见到过的事物，如是没有见过的事物，则将其印入脑海中。自适应共振理论模型在网络内部设有竞争网络，计算当前输入信息与已存模型中哪个最相似。如最相似度超过一定阈值，则达到识别模式的目的。如当可输入信息与所有已存模型都不够相似，则判定为新模式，并为其建模与存储。

RBF网络

竞争学习

竞争学习（competitive learning）是神经网络中一种常用的无监督学习策略，在使用该策略时，网络的输出神经元相互竞争，每一时刻只有一个竞争获胜的神经元被激活，其他神经元的状态被抑制。这种机制亦称“胜者通吃”（win-take-all）原则。有了竞争机制，人工神经元网络可以实现聚类等功能，一些典型的网络模型如自适应共振理论（Adaptive Resonance Theory），自组织特征映射等都属于具有竞争功能的非监督学习人工神经元网络。

ART网络

SOM网络

自组织特征映射（Self Organization Feature mapping SOF）是Kohonen提出的一种将高维空间中的数据映射到低维空间的一种神经元网络，而实现映射的同时要保持数据在原高维空间的相似性。这是指原数据在高维空间较相近，则它们的映象在低维空间中也应相近。这种网络结构的特点是输出结点数量众多，并按一定规则排列。它们接受高维信号，并在某个输出结点中得到高响应。输入高维信号相近，则高响应的输出结点也应相近。

Elman网络

递归神经网络（recurrent/recursive neural networks）允许网络中出现环形结构，从而可让一些神经元的输出反馈回来作为输入信号。使得网络在t时刻的输出状态不仅与t时刻的网络状态有关，还与t-1时刻有关，从而能处理与时间有关的动态变化。 Elman网络是最常用的递归神经网络之一。

Hebb学习

我们外在的行为是神经网络接受刺激之后产生的反应。神经元与神经元之间的连接有强有弱，而这种强弱是可以通过学习（训练）来不断改变的。如果两个神经元总是相关连的受到刺激或者反应，他们的连接就会一次一次的被加强。这也就是Hebb学习法了。

Hebb规则： Hebb是神经生理学家, 在1949年提出一种假没，认为脑细胞中突触强度根据其感受到的经验改变。他因此提出这种突触强度的改变与神经在触发前后突触之间的相关成正比。由于在Hopfield模型中采用的联接规则与Hebb的修改相比，因而在人工神经之网络中广泛使用的规则以Hebb冠名。这种规则除了在Hopfield模型中使用外，在非监督学习方法的人工神经元网络中广泛采用。
非监督Hebb学习方法：人工神经元网络也用来分析数据集内的一些规律，如方差分析，主分量分析等，由于其训练方法采用了Hebb规则，因而称为非监督Hebb学习方法。

通俗描述：巴甫洛夫的狗先摇铃铛，之后给一只狗喂食，久而久之，狗听到铃铛就会口水连连。这也就是狗的“听到”铃铛的神经元与“控制”流口水的神经元之间的连接被加强了。

Part 2 NN from scratch