裂缝识别

博客分类: tech 阅读次数:
CNN (1) 图像分割 (1)

裂缝识别

CNN (1) 图像分割 (1)

公路在使用过程中，总会因为行车、自然因素出现裂缝，这些裂缝如果不及时维护（填沥青）的话，可能会影响到车辆的正常通行。

可是真是环境总是变化多样的，光照、磨损会带来各种干扰或是消弭调裂缝本身的可见性。于是乎，机器识别达不到的正确率只能靠人力来弥补了。

但是这种单调、工作量大的活儿还是交给机器来做成本更低嘛。

所以我们就要用机器学习的思路来做啦～传统的就是基于特征，不管之后学习算法用的是SVM还是BP，第一步总归是人的脑力风暴来决定提取那些特征以及怎样提取。

可是现在有了深度学习就不一样了，输入的图片还是原原本本的样子，顶多是做一下压缩。

我们现在实现的模型也就是基于多层的卷积操作和pooling操作（有的地方译作池化）来逐渐“降维”，最终原来image大小的图就被一群方格代表了（我们的输出粒度是方格大小）。

而我现在又有想要把attention融进来的念头，毕竟卷积在做判断（softmax）的时候还是局部性的考虑，对有裂缝或是没裂缝如果说最后是有这个filter的话，应该说还是固定的，而如果能结合周围的方格状况综合考虑的话，就不算太死板。

Introduction

首先将原始图片划分为同等大小的方形区域，对这些block进行识别，可看做是粗粒度的pixel-wise图像标记，目前的标记只有两种：有裂缝、无裂缝。

在前期试验中，我们仅使用CNN可以很好地提取图片特征进行分类，但是：

因此，我们通过在CNN后增加probability inference模块改进算法：

Conditional Random Fields(CRF)用于pixel-wise的图像标记（其实就是图像分割）。把像素的label作为形成马尔科夫场随机变量且能够获得全局观测时，CRF便可以对这些label进行建模。这种全局观测通常就是输入图像。即在判断某一个方格时需要考虑整张图的情况，从而解决“噪点”和连接的问题。

输入图像： \(x=\{x_1,\dots,x_P\}\) $P$为像素数。

目标输出： \(y=\{y_1,\dots,y_B\},y_i \in L=\{l_1,l_2,\dots,l_L\}\) 因为我们判断的是每一方格是不是裂缝。因此这里的标签$L$目前只有两种。\(y_i\)即为第\(i\)个方格的标签。

主要参考论文：《Conditional Random Fields as Recurrent Neural Networks》

Github : CRF-RNN for Semantic Image Segmentation

Semantic Image Segmentation

1. 理论部分

Feature Extraction : CNN

此处输入图片的描述

##

我们的目标输出为总方格数$B$(blocks)的$D$维vectors矩阵， 相当于实现：\(img_h \times img_w \Longrightarrow block_h \times block_w \times D\)

执行5次pool_size=22的池化就相当于\(\frac {输入图片大小}{2^5}\),这样原来的640928就一步步变成了20*29。 相当于32 bits prediction 在对原始图像进行“缩放”的同时，我们实际上通过卷积操作提取每一方格内图像的标注向量annotation vector：

\[a=\{\mathbf a_1,\dots,\mathbf a_B\},\mathbf a_i \in \mathbb R^D\]

without considering the smoothness and consistency of the label assignment. 因此需要考虑pairwise data-dependant smoothing term. 作为CRF的一元势能量。

这一阶段要考虑的参数：

关于RNN

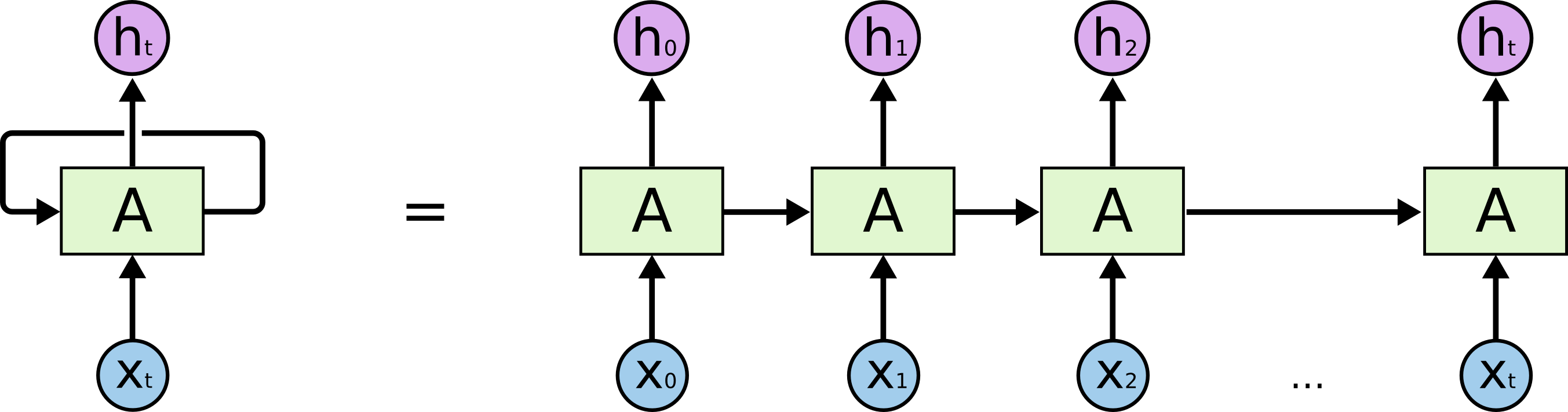
此处输入图片的描述

关于CRF(概率图模型)

下面来讲 CRF 用于 pixel-wise 的图像标记（其实就是图像分割）。当把像素的label作为形成马尔科夫场的随机变量，且能够获得全局观测时，CRF便可以对这些label进行建模。

CRF

图中的\(y_i\)为观测，即像素。

定义随机变量\(X_i\)是像素\(i\)的标签。

\[X_i \in L={l_1,l_2,...,l_L}\]

假设图\(G=(V,E)\)，其中\(V={X_1,X_2,\dots,X_N}\)，全局观测为（image）\(I\)。\((I,X)\)即基于Gibbs分布的CRF模型：

\[P(X=x|I)=\frac 1{Z(I)}exp(-E(x|I))\]
\(Z(I)\)是所有可能labeling的集合，保证$$P(X=x I)$$在0~1。

条件随机场图像分割能量函数的构造：

\[E(x)=\sum _i \varphi_u(x_i)+\sum _{i<j} \varphi_p(x_i.x_j)\]

这里的\(E\)可以理解为能量，也就是cost。其中\(\varphi_u(x_i)\)是将像素\(i\)标记为\(x_i\)的inverse likelihood，\(\varphi_p(x_i.x_j)\)是将\(i\)、\(j\)同时标记为\(x_i\)、\(x_j\)的能量。

Recall the HMM :

在做NLP的Part-of-Speech tagging（adj. n. v. prep. adv.）的时候，下层的是它的观测(word)，上层就是 word对应的词性label。

\[p(l,s)=p(l_1)\prod_i p(l_i|l_{i-1})p(\omega_i|l_i)\]

(transition probability x emission probability)。

对比一下的话，CRF可以使用更多global features，而HMM只考虑前一个label。比如POS任务里，句子结尾的一个问号增大第一个词标记为动词的概率。或许看下面这张图会领会更多：

1d3f9cefc0de33cfebe71bbc237ccc6b_b.png-80.1kB

关于CRF更详细的内容可参考论文： 《 An introduction to conditional random fields 》

2. 网络构建

\[\varphi_p(x_i.x_j)=\mu (x_i,x_j)\sum_{m=1}^M \omega ^{(m)}k_G^{(m)}(\mathbf f_i,\mathbf f_j)\]

其中

\[k^{(m)}(\mathbf f_i,\mathbf f_j)=\exp(-\frac 12(\mathbf f_i-\mathbf f_j)^{\mathrm T}\varLambda^{(m)}(\mathbf f_i-\mathbf f_j))\]

\(\mathbf f_i\)是像素\(i\)的feature vector，这里是从原图片中提取的。 Potts Model ： \(\mu(x_i,x_j)=[x_i \neq x_j]\) 是对位置接近的相似像素标记不同的惩罚项。

Mean-field = CNN + softmax

基于平均场，使用更简单的分布\(Q(\mathbf X)\)来逼近CRF的\(P(\mathbf X)\)：

\[U_i(l)=-\varphi_u(\mathbf X_i=l) \\ Z_i=\sum_l \exp (U_i(l))\]

1. 首先初始化：

对每个像素上的所有label做softmax：

\[Q_i(l) \leftarrow \frac 1{Z_i}\exp (U_i(l)) \\\]

等同于softmax ： \(h_j = \frac{e^{z_j}}{\sum{e^{z_i}}}\)

由于这里不涉及其他参数，因此梯度在经过softmax的反向计算后直接传给unary potentials。

\[\frac{\partial h_{j}}{\partial z_{k}} = h_{j}\delta_{kj}-h_{j}h_{k}\]

2. Message passing:

对\(Q\)进行\(M\)个高斯滤波：

\[Q_j(l) \leftarrow \sum_{i \neq j} k^{(m)}(\mathbf f_i,\mathbf f_j)Q_j(l)\]

补充： (1) 如果是稀疏条件随机场，那么我们构造图模型的边集合E就是：每对相邻的像素点间可以构造一条边。当然除了4邻域构造边之外，你也可以用8邻域模型。 (2) 全连接条件随机场与稀疏条件随机场的最大差别在于：每个像素点都与所有的像素点相连接构成连接边。这就恐怖了，如果一张图像是\(100 \times 100\)，那么就相当于有10000个像素点，因此如果采用全连接条件随机场的话，那么就会构造出约\(10000 \times 10000\)条边。如果图像大小再大一些，那么就会变得非常恐怖，普通条件随机场推理算法，根本行不通。

此处输入图片的描述

此处输入图片的描述

3. Weighting Filter Outputs

为每个标签计算\(M\)个filter输出的weighted sum ，可以看成是有\(M\)个输入channel、1个输出channel的卷积操作。

\[Q_i(l) \leftarrow \sum _m \omega ^{(m)}Q_i^{(m)}(l)\]

考虑到识别对象，这里针对每个标签使用不同的spatial kernel和bilateral kernel权重，作者举的例子是bilateral filter 在识别自行车上很重要（此时颜色的相似性很关键），但识别电视机就不那么重要（电视机有各种颜色）。

4. Compatibility Transform

\[Q_i(l) \leftarrow \sum _{l' \in \mathcal L}\mu (l,l')Q_i(l)\]

至此完成了构造\(\varphi_p(x_i,x_j)\)的任务。

5. unary-compatibility transform

计算\(E(\mathbf x)\)：

\[Q_i(l) \leftarrow U_i(l)-Q_i(l)\]

6. Normalization：softmax

计算$$P(\mathbf X=\mathbf x \mathbf I)$$：
\[Q_i(l) \leftarrow \frac 1{Z_i}\exp (Q_i(l))\]

Iterable Mean-field = RNN

\[f_{\theta}(U,Q_{in},I) \\ \theta=\{\omega^{(m)},\mu(l,l')\},\\ m\in \{1,\dots,M\},l,l' \in \{l_1,\dots,l_L\}\]

迭代结构等同于RNN，假设迭代T次：

3. Caffe上的实现

Caffe 是由伯克利大学视觉和学习中心开发的一种深度学习框架。在视觉任务和卷积神经网络模型中，Caffe 格外受欢迎且性能优异。

输入图像：

\(x=\{x_1,\dots,x_P\}\) $P$为像素数。

目标输出：

\[y=\{y_1,\dots,y_B\},y_i \in L=\{l_1,l_2,\dots,l_L\}\]

因为我们判断的是每一方格是不是裂缝。因此这里的标签$L$只有两种。$y_i$即为第$i$个方格的标签。

自己写Python层作为输入层

road_layer.py

self.x = np.load(os.path.join(CACHE_PATH, 'x_{}.npy'.format(self.split)))
self.y = np.load(os.path.join(CACHE_PATH, 'y_{}.npy'.format(self.split)))

生成训练网络

net.py生成网络结构文件

    n.data, n.label = L.Python(module='road_layer', layer='ROADSegDataLayer',
            ntop=2, param_str=str(pydata_params))

    # the base net
    n.conv1_1, n.relu1_1 = conv_relu(n.data, 32, ks=5)
    n.conv1_2, n.relu1_2 = conv_relu(n.relu1_1, 32, ks=5)
    n.pool1 = max_pool(n.relu1_2)

    n.conv2_1, n.relu2_1 = conv_relu(n.pool1, 64)
    n.conv2_2, n.relu2_2 = conv_relu(n.relu2_1, 64)
    n.pool2 = max_pool(n.relu2_2)

    n.conv3_1, n.relu3_1 = conv_relu(n.pool2, 128)
    n.conv3_2, n.relu3_2 = conv_relu(n.relu3_1, 128)
    n.pool3 = max_pool(n.relu3_2)

    n.conv4_1, n.relu4_1 = conv_relu(n.pool3, 256)
    n.conv4_2, n.relu4_2 = conv_relu(n.relu4_1, 256)
    # n.conv4_3, n.relu4_3 = conv_relu(n.relu4_2, 512)
    n.pool4 = max_pool(n.relu4_2)

    n.conv5_1, n.relu5_1 = conv_relu(n.pool4, 256)
    n.conv5_2, n.relu5_2 = conv_relu(n.relu5_1, 256)
    # n.conv5_3, n.relu5_3 = conv_relu(n.relu5_2, 512)
    n.pool5 = max_pool(n.relu5_2)

    n.score = conv(n.pool5, 1)
    n.loss = L.SigmoidCrossEntropyLoss(n.score, n.label)
    # n.loss = L.MultiStageMeanfield()

分别为一次导入的图片个数，channel，heigth ，width。

Solver 优化

此处的SGD指mini-batch gradient descent，关于batch gradient descent, stochastic gradient descent, 以及 mini-batch gradient descent的具体区别就不细说了。现在的SGD一般都指mini-batch gradient descent。 SGD就是每一次迭代计算梯度，然后对参数进行更新，是最常见的优化方法了。 此处主要说下SGD的缺点：（正因为有这些缺点才让这么多大神发展出了后续的各种算法）

损失平面等高线：

损失平面等高线

在鞍点处的比较：

在鞍点处的比较

在Deep Learning中，往往loss function是非凸的，没有解析解，我们需要通过优化方法来求解。solver的主要作用就是交替调用前向（forward)算法和后向（backward)算法来更新参数，从而最小化loss，实际上就是一种迭代的优化算法。

到目前的版本，caffe提供了六种优化算法来求解最优参数，在solver配置文件中，通过设置type类型来选择。 在训练多通道图片时，此处最好需要有一个meanfile参数。.binaryproto

 train_net: "train.prototxt"
# train_net: "TVG_CRFRNN_new_deploy.prototxt"
test_net: "val.prototxt"
test_iter: 16
test_interval: 500
base_lr: 5e-4
lr_policy: "fixed"
momentum: 0.99
type: "Adam"
weight_decay: 0.0005
display: 100
max_iter: 1000
snapshot: 1000
snapshot_prefix: "snapshot/train"
solver_mode: GPU

This parameter indicates how the learning rate should change over time. This value is a quoted string.

  1. Options include:

训练caffemodel

../CRFasRNN-merge/caffe-master/build/tools/caffe train -solver solver.prototxt


solver = caffe.SGDSolver('models/bvlc_reference_caffenet/solver.prototxt')

整合crfasrnn

net.params : a vector of blobs for weight and bias parameters

net.params['conv1_1'][0] contains the weight parameters, an array of shape (32, 1, 5, 5) net.params‘conv’ contains the bias parameters, an array of shape (3,)

solver = caffe.SGDSolver('solver.prototxt')
solver.net.copy_from('pretrained_param_file')
[...]

## control layer's initialization
halt_training = False
for layer in solver.net.params.keys():
  for index in range(0, 2):
    if len(solver.net.params[layer]) < index+1:
      continue

    if np.sum(solver.net.params[layer][index].data) == 0:
      print layer + ' is composed of zeros!'
      halt_training = True

if halt_training:
  print 'Exiting.'
  exit()

To launch one step of the gradient descent, that is a forward propagation, a backward propagation and the update of the net params given the gradients (update of the net.params[k][j].data) :

solver.step(1)

MultiStageMeanfieldLayer

4. 细节

Loss Function

average intersection over union(IU)

Normalization techniques

rectified linear unit (ReLU)

5. 环境搭建

安装python依赖库：

    sudo pip install -r requirements.txt

测试

    #!/bin/bash

    TOOLS=../../caffe/build/tools
    WEIGHTS=TVG_CRFRNN_COCO_VOC.caffemodel
    SOLVER=TVG_CRFRNN_new_solver.prototxt

    $TOOLS/caffe train -solver $SOLVER -weights $WEIGHTS -gpu 0

Debug

  1. cuda
    libcudart.so.7.0: cannot open shared object file: No such file or directory

    sudo ldconfig /usr/local/cuda-7.5/lib64
  1. Python
    Unknown layer type: Python (known types: AbsVal, Accuracy, ArgMax, BNLL, Concat, ContrastiveLoss, Convolution, Crop, Data, Deconvolution, Dropout, DummyData, Eltwise, Embed, EuclideanLoss, Exp, Filter, Flatten, HDF5Data, HDF5Output, HingeLoss, Im2col, ImageData, InfogainLoss, InnerProduct, LRN, Log, MVN, MemoryData, MultiStageMeanfield, MultinomialLogisticLoss, PReLU, Pooling, Power, ReLU, Reduction, Reshape, SPP, Sigmoid, SigmoidCrossEntropyLoss, Silence, Slice, Softmax, SoftmaxWithLoss, Split, TanH, Threshold, Tile, WindowData)

修改Makefile.config

WITH_PYTHON_LAYER := 1

重新make caffe

rm -rf ./build/*
make all -j8

8 is the number of parallel threads for compilation (a good choice for the number of threads is the number of cores in your machine).

2.1 build errors:undefined cv::imread() cv::imencode() …

cmake

本文由 Rowl1ng 创作，采用 知识共享署名4.0 国际许可协议进行许可
本站文章除注明转载/出处外，均为本站原创或翻译，转载前请务必署名
本文会经常更新，最后编辑时间为:2015-10-18 11:12:00